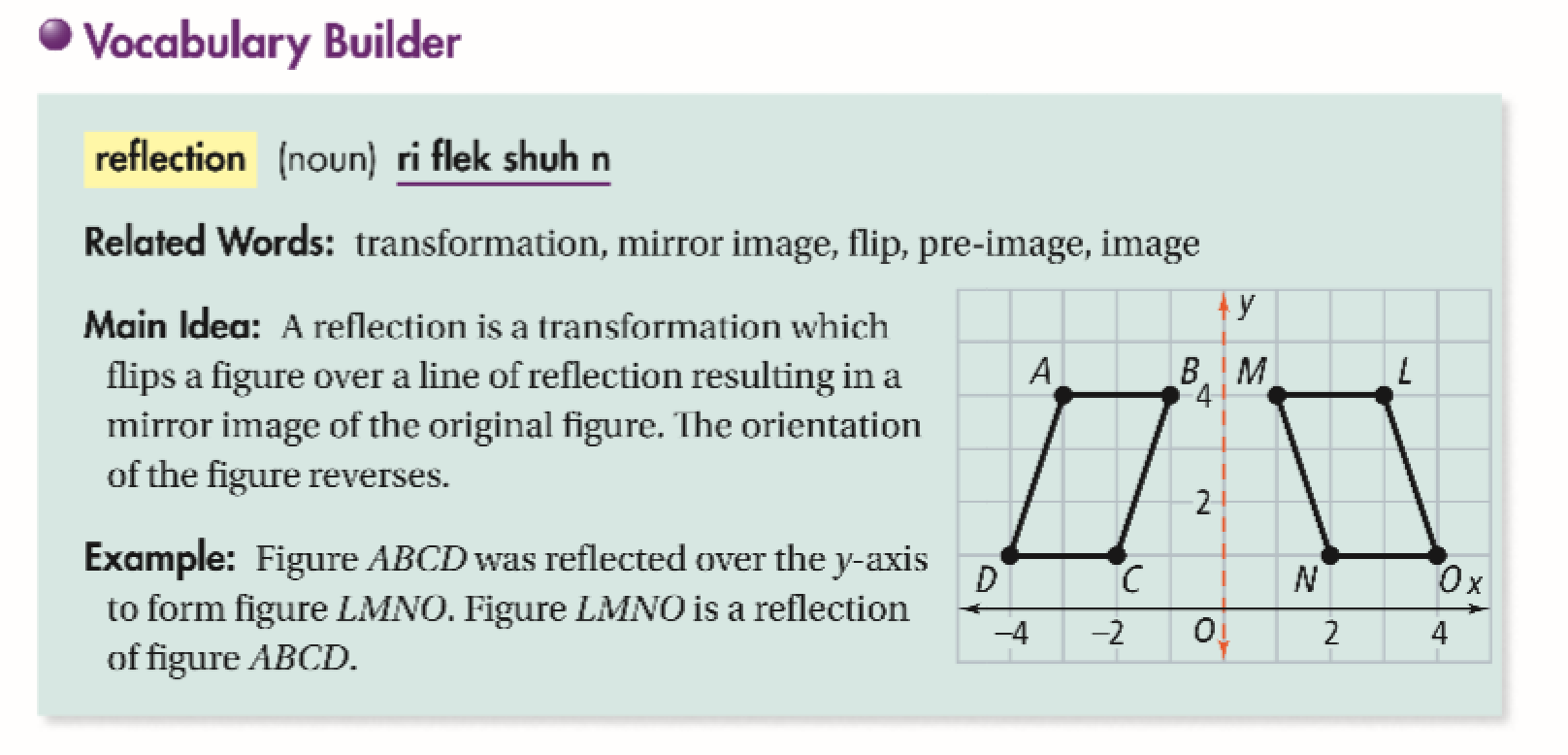
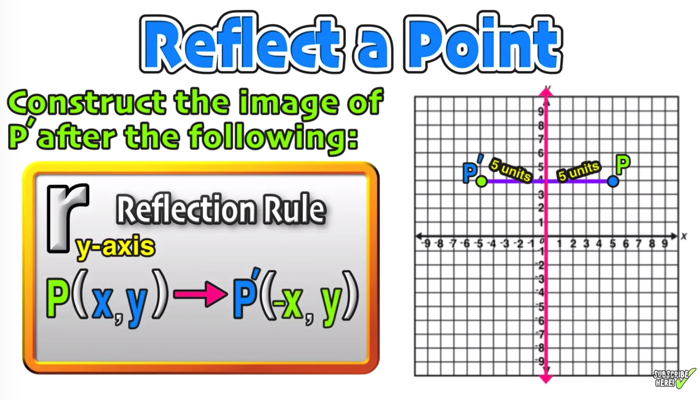
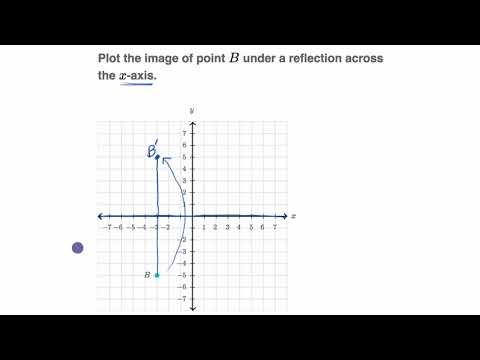
Click and drag the blue dot to see it's reflection across the line y=x (the green dot) Pay attention to the coordinates How are they related to each other?We need an m x n matrix A to allow a linear transformation from Rn to Rm through Ax = b In the example, T R2 > R2 Hence, a 2 x 2 matrix is needed If we just used a 1 x 2 matrix A = 1 2, the transformation Ax would give us vectors in R118 B 6 A point has the coordinates (0, k) Which reflection of the point will produce an image at the same coordinates, (0, k)?

Graph The Image Of The Polygon After A Reflection In Chegg Com
How to do a reflection across the line y=x
How to do a reflection across the line y=x-A'B'C' was constructed using ABC and line segment EH For transformation to be reflection, which statements must be true?Background Tutorials Use a pair of perpendicular number lines, called axes, to define a coordinate system, with the intersection of the lines (the origin) arranged to coincide with the 0 on each line and a given point in the plane located by using an ordered pair of numbers, called its coordinates



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative
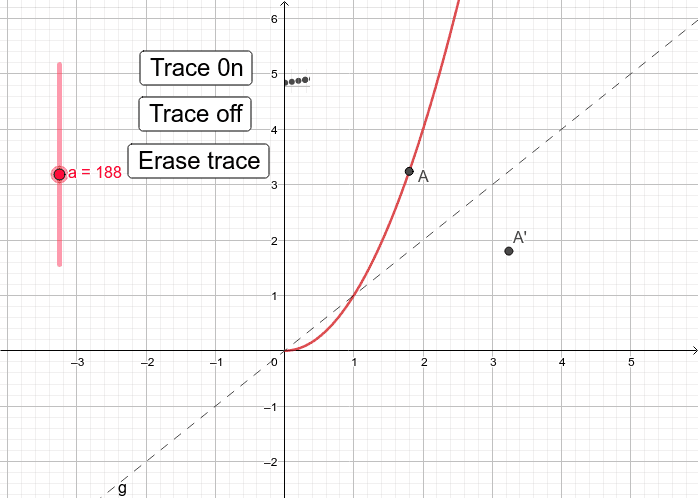
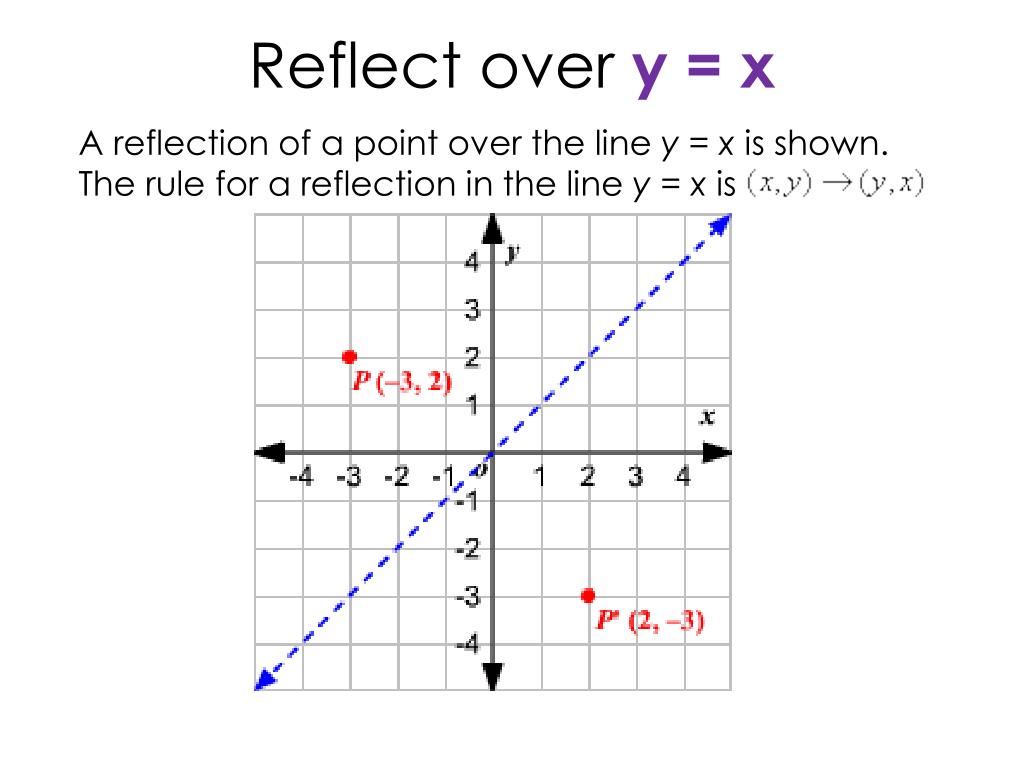
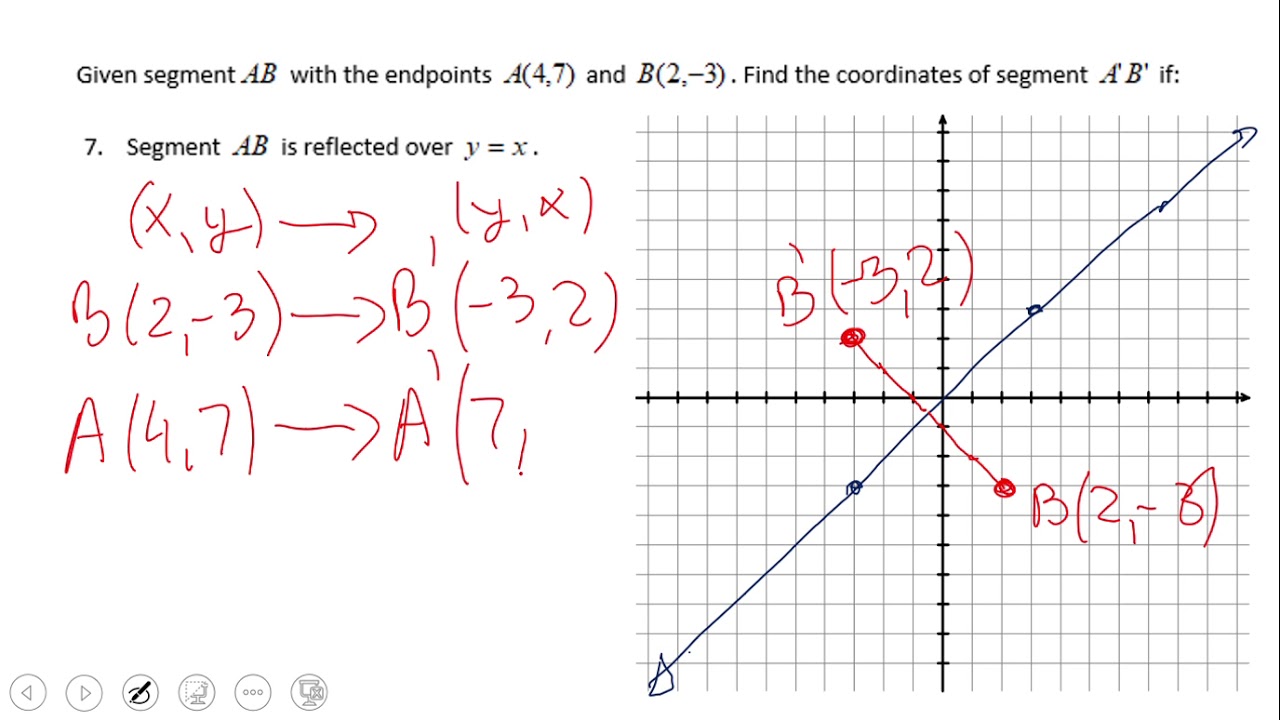
Reflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the23 Questions Show answers Q Flipping a figures is a Q Is the picture being reflected in the yaxis or xaxis?Reflection about the line y = x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure Let us consider the following example to have better understanding of reflection
Let T be the linear transformation of the reflection across a line y=mx in the plane We find the matrix representation of T with respect to the standard basisReflection Over the Line y=x In this video, you will learn how to do a reflection over the line y = x The line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1Question (b) The transformation k is the reflection in the line y = x 7 By using the translation h that maps the point (0,7) to the origin, and its inverse h1, find the affine transformation k in the form k(x) Bxb, where B is a 2 x 2 matrix and b is a column vector with two components
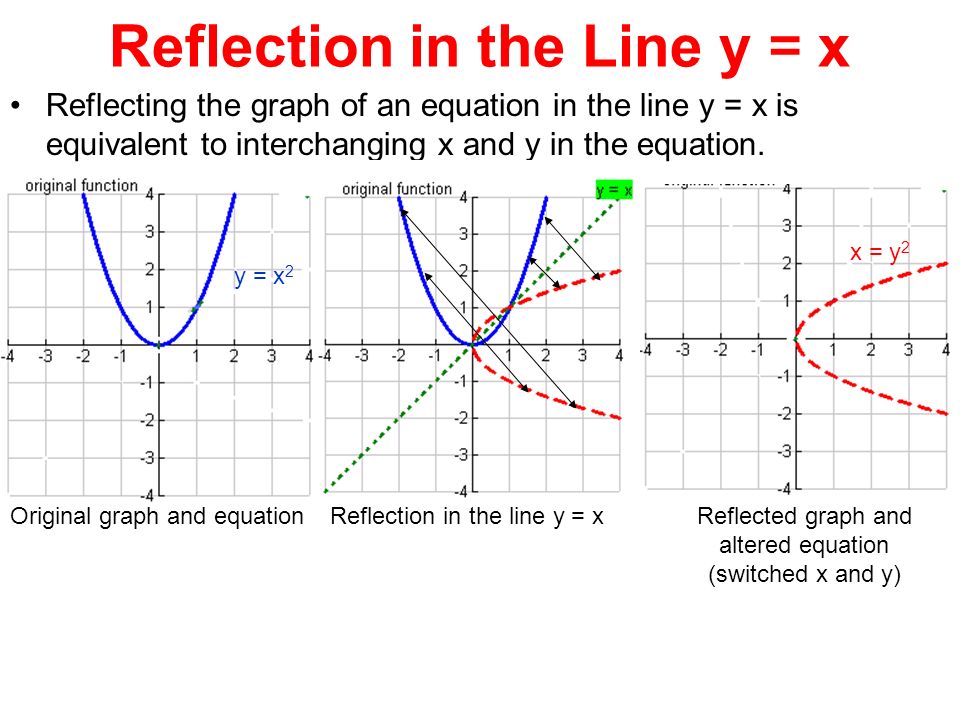
line segments I end this segment i n over here and T oh this is T oh here are reflected over the line y is equal to negative X minus 2 so this is the line that they're reflected about this dashed purple line and it is indeed y equals negative X minus 2 this right over here is in slopeintercept form the slope should be negative 1 and we see that the slope of this purple line is Reflection in a Line 4 Reflecting over the line y = x or y = x (the lines y = x or y = x as the lines of reflection) When you reflect a point across the line y = x, the xcoordinate and the ycoordinate change placesTo reflect points across the line {eq}y=x {/eq}, we must swap the coordinates and change their signs To see why this works, consider the first and third quadrants Reflecting the first quadrant



Math Alive Geometry 1




Reflection Rules How To W 25 Step By Step Examples
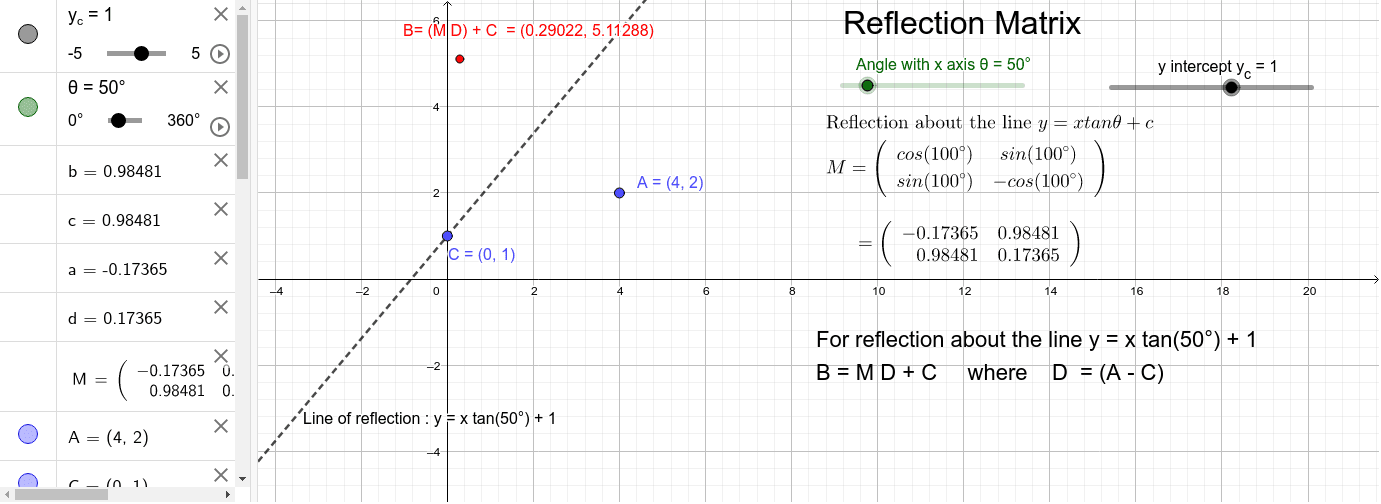
Get the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlphaSince point A is located three units from the line of reflection, we would find the point three units from the line of reflection from the other side The yvalue will not be changing, so the coordinate point for point A' would be (0, 1) Repeat for points B and C In the end, we found out that after a reflection over the line x=3, theTo reflect along a line that forms an angle θ with the horizontal axis is equivalent to rotate an angle − θ (to make the line horizontal) invert the y coordinate rotate θ back Further, y = mx implies tanθ = m, and 1 m2 = 1 cos2θ Then, assumming you know about rotation matrices, you can write




Reflection Over Y X Math Geometry Showme




Graph The Image Of The Polygon After A Reflection In Chegg Com
Reflections flip a preimage over a line to create the image In this lesson we'll look at how the reflection of a figure in a coordinate plane determines where it's located A reflection is a type of transformation that flips a figure over a line The line is called the line of reflection, or the mirror lineReflection in the line y = x y = x is the equation of the line which makes an angle of 45° with the positive direction of X axis Then, slope of the line, m 1 =Q Reflect over xaxis Which point would be at (3,



Reflecting In The Line Y X 2 Geogebra




Reflection Mathbitsnotebook A1 Ccss Math
Reflection about line y=x The object may be reflected about line y = x with the help of following transformation matrix First of all, the object is rotated at 45° The direction of rotation is clockwise After it reflection is done concerning xaxisQuestion Find the equation of the images of the following lines when the reflection line is the yaxis a) y = x6 b) y = 2Thus for y = f ( x), the reflection about the line y = x is accomplished by x = f ( y) For example, the reflection about the line y = x for y = x 2 is the equation x = y 2 Hope it helps If the curve is complicated, you can just take particular, interesting points and switch the coordinates



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa




Why Do Points Get Exchanged When Reflected Across Line Y X Quora
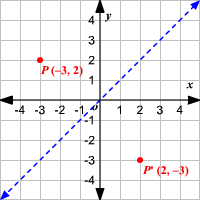
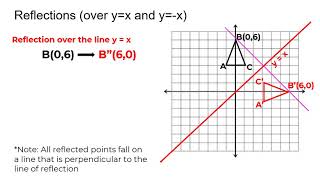
A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection A reflection of a point over the line y = − x y = −x is shown The Line Y=X Another common reflection occurs when a preimage is reflected over the line y = x Examine the drawing below to see the relationship between the coordinates of the preimage and image Notice that the xand yvalues are reversed In otherwords, the xvalue of the preimage maps onto the yvalue of the image and vice versaCheck all that apply The line of reflection, EH, is the perpendicular bisector of BB', AA', and CC'



Reflect Function About Y Axis F X Expii



1
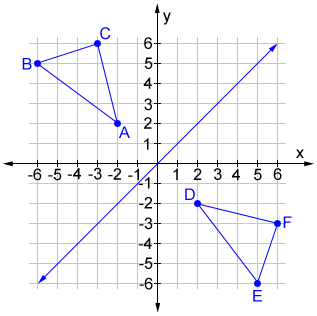
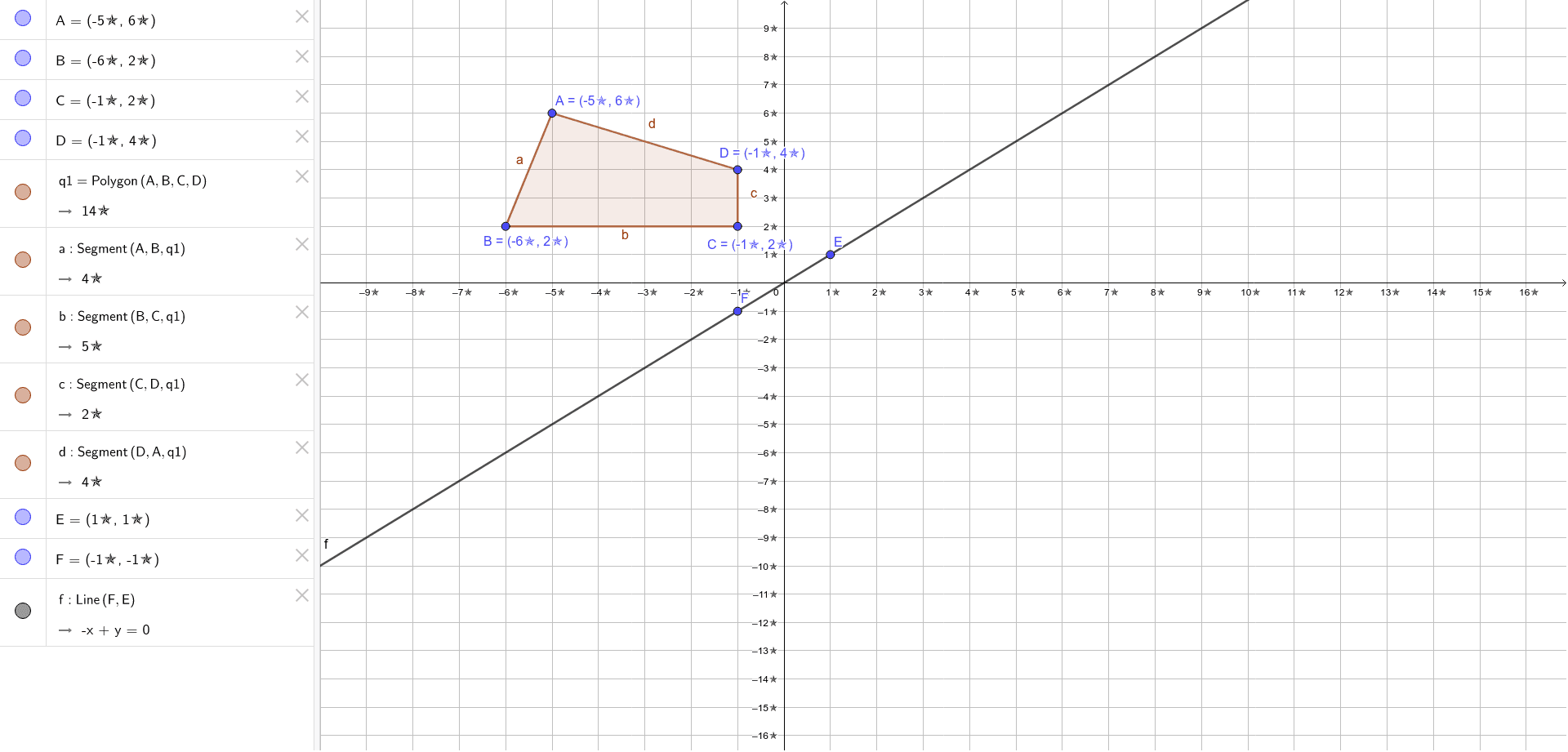
Find the equation of the images of the following lines when the reflection line is the yaxis a) y = x6 b) y = 2;A reflection of the point across the xaxis a reflection of the point across the yaxis a reflection of the point across the line y = x a reflection of the point across the line y =A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6) Triangle DEF has vertices D (2, 2), E (5, 6), and F (6, 3)




Transformations Of Graphs



1 Geometry Ms Singarajah 7
Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)A reflection of a point over the line y x is shown This means all of the xcoordinates have been multiplied by 1 The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point but leave the xvalue the same A x y in y x b x y in y x c x y in xA shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate




The Equation Of A Line Reflected About Another Line Mathematics Stack Exchange



Ppt Reflect Over Y X Powerpoint Presentation Free Download Id
Reflection in the line y = 0 ie, in the xaxis The line y = 0 means the xaxis Let P be a point whose coordinates are (x, y) Therefore, when a point is reflected in the xaxis, the sign of its ordinate changes SHOW ANSWER In the most simple terms, the solution would be y=x because this line, which travels straight through the origin, touching points (1,1) and (2,2), is the only given line that passes through the center of the given reflection After drawing the line, you can see that points C and C', B and B', and A and A' are exactly oppositeWhen a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place Similarly, when a point is reflected across the line y = x, the xcoordinates and ycoordinates change their place and are negated



Solution After A Reflection In The Line Y X 8 3 Is The Image Of Point Q What Is The Original Location Of Point Q



1
Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x) Reflection about the line #y = x# The effect of this reflection is to switch the x and y values of the reflected point The matrix is #A = ((0,1),(1,0))# CCW rotation of a point For CCW rotations about origin by angle #alpha# #R(alpha) = ((cos alpha, sin alpha),(sin alpha , cos alpha))# If we combine these in the order suggestedTutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT




How To Find A Reflecting Line Dummies
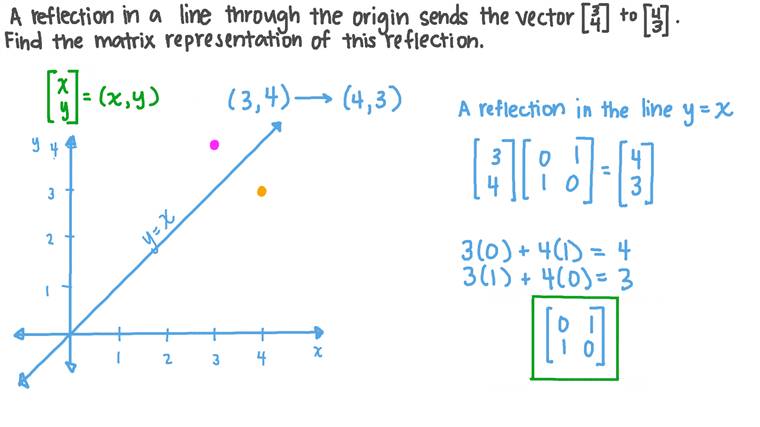



Lesson Linear Transformations In Planes Reflection Nagwa
What are the coordinates of the image of vertex G after a reflection across the line y=x? In some cases, the line of reflection may be on the edge – or even inside – the figure Three common ways to reflect figures are over the xaxis, yaxis, and the line y=x Something to notice as we look at these is that the signs of the coordinates change For example, when a figure is reflected over the xaxis, notice the ycoordinates If you need the visible reflection then you can use package pstoptic Run the example with pdflatex shellescape This allows you to reflect the function on an arbitrary line and without being restricted in your choice of compilers a=b=1 is the x=y line




Reflections Geometry Abroad




Reflection Over The Line Y X Geogebra
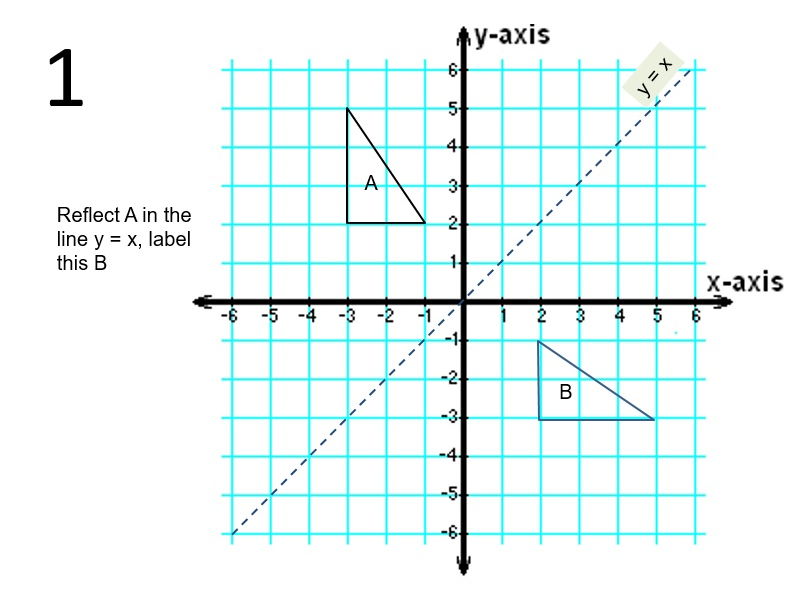
Begin with the reflection though the yaxis Try to guess which ordered pair rule will produce the desired image Next try a reflection through the xaxis For this step you will need to drag the red X to the xaxis (a blue open circle point is plotted as a suggestion) Now the hard part Can you match which rules reflect over the lines y=x and (a) Write the equation of a line that intersects the negative xaxis and the positive yaxis at points not equidistant from the origin (0, 0) (b) Draw the line (c) Draw the line that is the reflection of your line across the line y=x (d) Find the equation of the line drawn in Part (c) Do not convert fractions, if any, to decimalsFlip over a line;
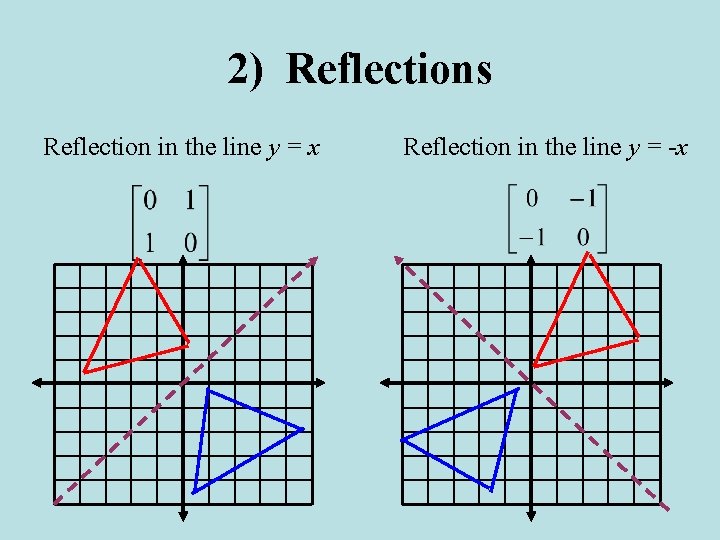



4 4 Transformations With Matrices 2 Reflections And



Why Aren T Reflected Lines Perpendicular Meaning Why Are Their Slopes Negative Not Negative Reciprocals Enotes Com
Reflection Transformations in 3Space Like in $\mathbb{R}^2$ , we can take some vector $\vec{x} = (x, y, z)$ and reflect it This time we will be reflecting over planes instead ofVirtual Nerd's patentpending tutorial system provides incontext information, hints, and links to supporting tutorials, synchronized with videos, each 3 to 7 minutes long In this nonlinear system, users are free to take whatever path through the material best serves their needs These unique features make Virtual Nerd a viable alternative to private tutoring A reflection of a point, a line, or a figure in the X axis involved reflecting the image over the x axis to create a mirror image In this case, the x axis would be called the axis of reflection Math Definition Reflection Over the Y Axis




Solution What S The Result When We Reflect Y Sin X Twice Trigonometry Triangles To Functions Underground Mathematics




Reflecting Shapes Article Reflections Khan Academy
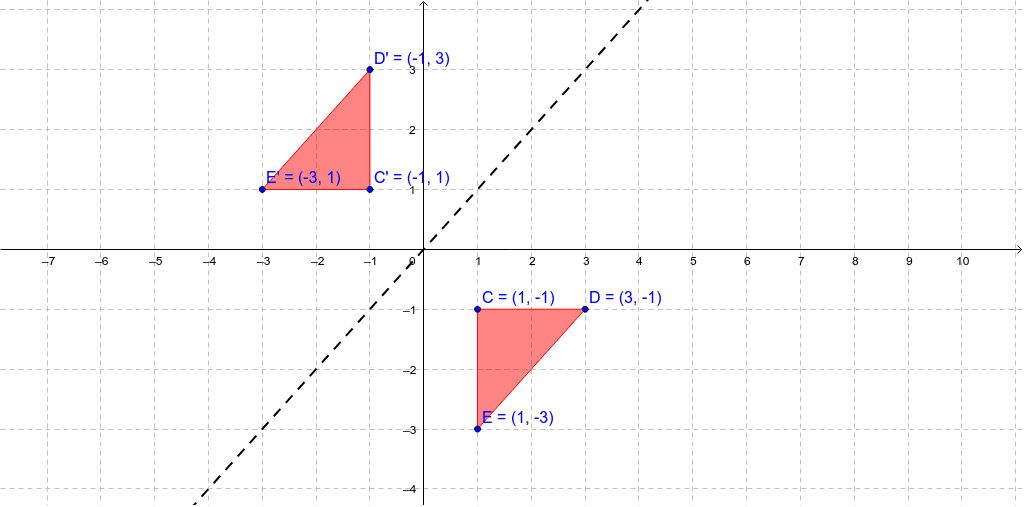
This website and its content is subject to our Terms and Conditions Tes Global Ltd is registered in England (Company No 0172) with its registered office at 26 Red Lion Square London WC1R 4HQReflections A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line The fixed line is called the line of reflection We have to identify the rules of reflection Firstly, the rule for reflecting a point about the line y=x is While reflecting about the line y=x, we get the reflected points by swapping the coordinates So, Option 3 is correct Now, the rule for reflecting a point about the line y= x is



Reflection Of A Point In A Line Msrblog
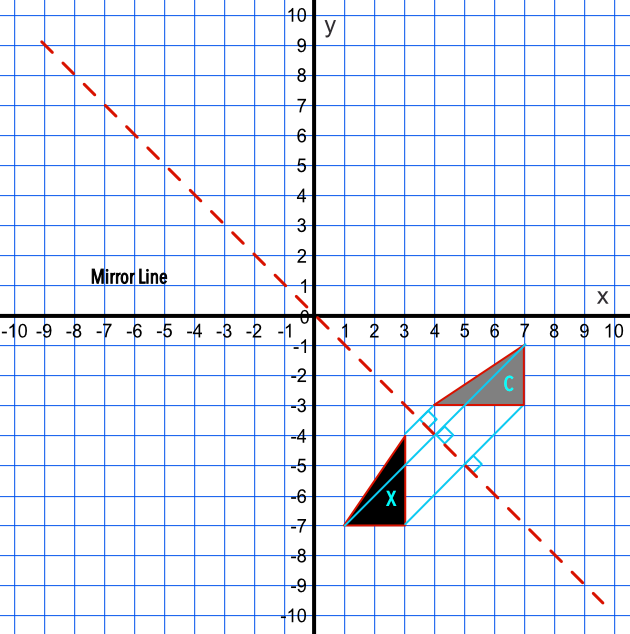



Reflection
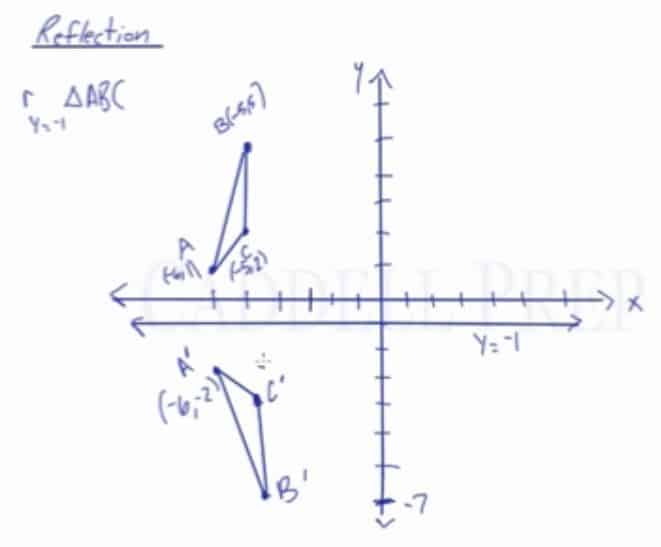
There are at least two ways of doing so Method 1 The line y = 3 is parallel to xaxis Let the required image is P′ By common sense, we know (Distance between the line y = 3 and point P) = (Distance between line y= 3 and point P′) Since line joinThis lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitter




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflections Through The Axes And The Lines Y X And Y X Geogebra




Reflecting Shapes Video Reflections Khan Academy



Reflection Over The X And Y Axis The Complete Guide Mashup Math




How To Find A Reflection Image




Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math
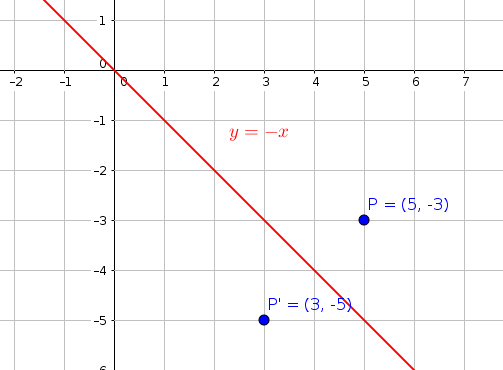



What Is The Reflection Image Of 5 3 In The Line Y X Socratic



Reflection Over The Line Y X Math Showme




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
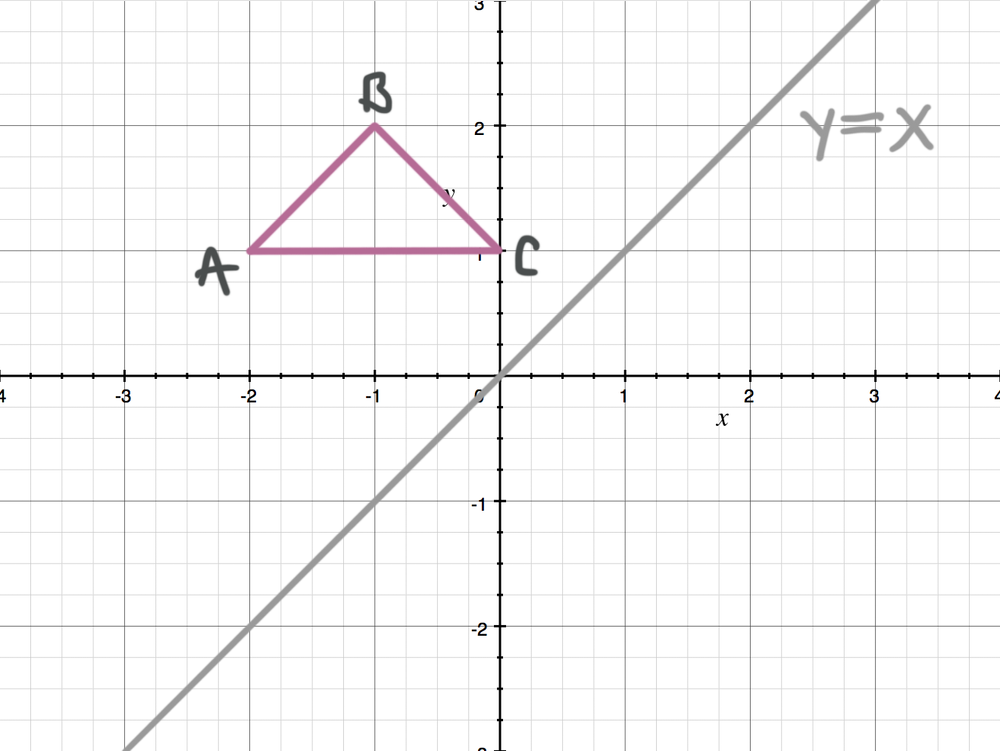



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflection Over Y 2 With Rule Educreations




Reflection Transformation



Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line




Picture Of Reflection Across Y Axis Reflection Math Reflection Math



Reflection Over Y X And Y X Youtube




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative



Reflection



Reflection Matrix About Line Y X Tan 8 C Geogebra




Reflections Read Geometry Ck 12 Foundation




Reflection Mathbitsnotebook A1 Ccss Math




Lesson On Line Of Reflection Y X




More Reflections Easing The Hurry Syndrome




Reflections Across Y X Geogebra




How To Reflect A Graph Through The X Axis Y Axis Or Origin



Transformations Mathematics Gcse Revision




How To Find A Reflection Image
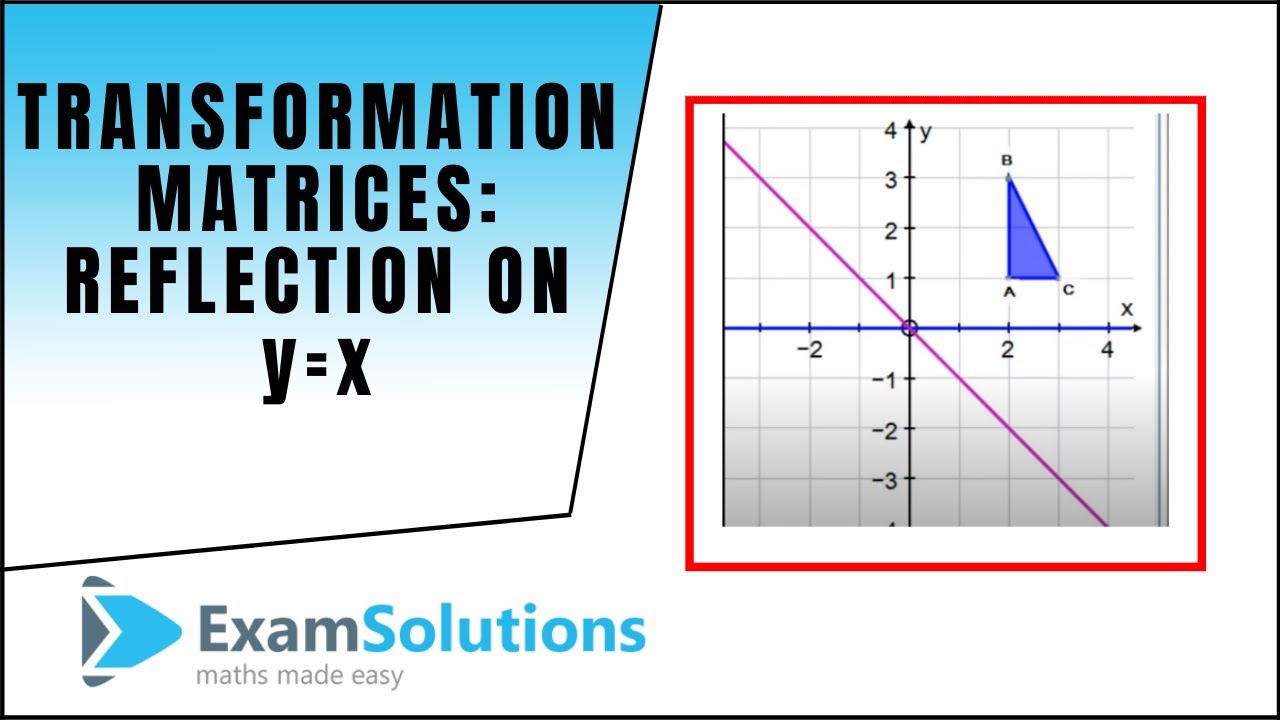



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube



Learn About Reflection Over A Horizontal Or Vertical Line




Transformation Reflection Over The Line Y X Youtube
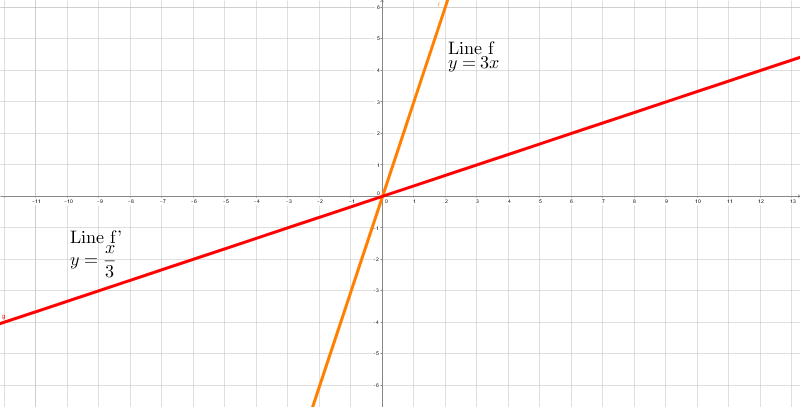



Reflection Brilliant Math Science Wiki




Reflection Rules How To W 25 Step By Step Examples




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Reflection Over The Y X Line Youtube



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora



What Is The Image Of 2 5 Reflected Across X 2 Socratic



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com



Reflecting Points Video Reflections Khan Academy



Reflection Across The Line Y X Geogebra



Reflection In The Line Y X Geogebra



1




Reflection Over The Line Y X Math Showme



What Does It Mean To Reflect Over The Y X Line Quora




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Rules For Reflections Read Geometry Ck 12 Foundation



Diagonal Reflections In The Line Y X Teaching Resources
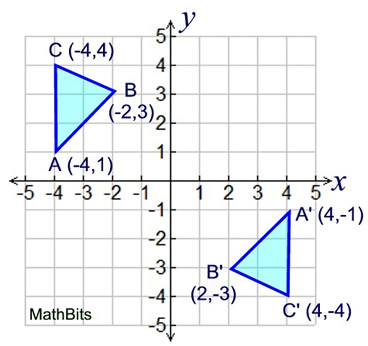



Reflection Mathbitsnotebook Jr




Linear Transformations With Matrices Lesson 10 Reflection In The Line Y X Youtube




Reflection Mathbitsnotebook A1 Ccss Math



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N
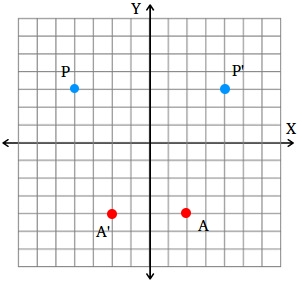



How To Find A Reflection Image




Common Reflections Key Stage 3
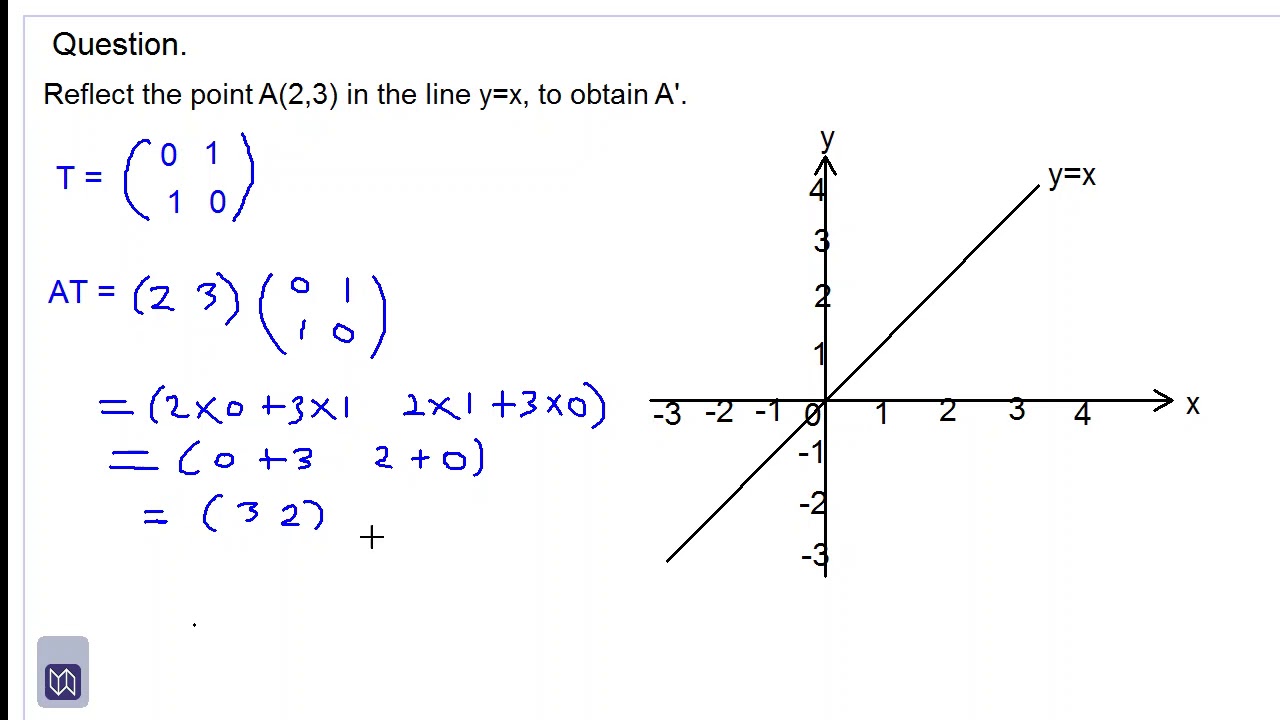



Transformation Matrix For Reflection In Y X Youtube
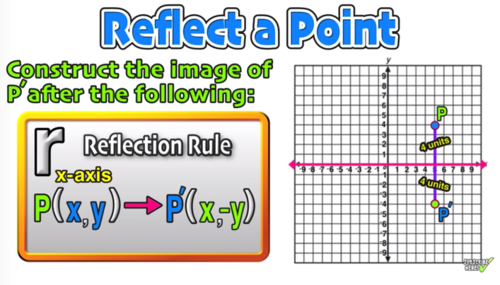



Reflection Over The X And Y Axis The Complete Guide Mashup Math



Math Alive Geometry 1




Picture Of Reflection In The Line Y X Reflection Math Math Reflection




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Reflections




Reflection In Geometry Examples Solutions Videos Worksheets Games Activities




Suppose The Equation Of Line S Is Y 2 What Are The Coordinates Of C Of Delta A B C For R S A 1 4 B 1 3 C 3 5 D 2 5 Study Com



Q Tbn And9gctvjthqkdwbpqfxmfukfqyrhm8wtlbtfnfu2u0osqggs0pct8ms Usqp Cau




How To Reflect A Graph Through The X Axis Y Axis Or Origin




Learn About Reflection Over The Line Y X Caddell Prep Online




Describing A Reflection Key Stage 2




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor



Reflection Over The Y X Line Youtube




Reflection Over A Line Expii




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection In The Line Y X Transformation Matrix Youtube




Reflection Mathbitsnotebook A1 Ccss Math




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflection In The Line Y X Geogebra




Algebraic Representations Of Reflections




Reflection Over The Line Y X Youtube




Reflection Rules How To W 25 Step By Step Examples



0 件のコメント:
コメントを投稿